3. Strukturelle Teleologie (ab 19. Jhd.)

Offenbar lässt sich die galileische Nomologie also nicht ohne Probleme auf lebende Wesen bzw. auf Menschen übertragen. Unweigerlich wird man an die aristotelische Vorstellung einer Entelechie als innere Antriebskraft des Verhaltens erinnert. Im Gegensatz zu toten Körpern wie Steine, deren Verhalten äußeren, allgemein gültigen Gesetzmäßigkeiten folgt, wird bei Lebewesen das Verhalten ja tatsächlich irgendwie „von innen heraus“ gesteuert oder zumindest maßgeblich beeinflusst.

Entropie – Zeitlich gerichtete Prozesse in der Thermodynamik

In der Welt der Physik sind Prozesse, die eine Art innere Dynamik beschreiben, längst bekannt, allerdings nicht auf der Ebene einzelner (materialer) Elemente, sondern auf der Ebene von Strukturen – also einer abgrenzbaren Menge von Elementen, die miteinander in Beziehung stehen.

Den ersten wissenschaftlichen Absatz lieferte hierzu die Mitte des 19. Jhd. entstandene Thermodynamik durch das Konzept der „Entropie„. Die sich damals entwickelnde Industrialisierung erforderte leistungsfähige Dampfmaschinen, die man ständig zu optimieren trachtete. Nicolas Leonard Sadi Carnot stellte 1824 dabei die These auf, dass die verfügbare Energie nicht von der Wärme (im Heizkessel), sondern von der Wärmedifferenz (zwischen Heizkessel und Kondensator) abhängt. Wenn Wärme von einem heißen in einen kalten Zustand übergeht, kann eine mechanische Kraft erzeugt werden. Robert Meyer formulierte 1841 ergänzend den ersten Hauptsatz der Thermodynamik, der besagt, dass in einem abgeschlossenen System Energie nicht verschwinden, sondern nur umgewandelt werden kann (mit der Wärmeenergie die beim Abkühlen von 1 g Wasser um 1 Grad Kelvin frei wird, könnte man einen Körper von 1 g Gewicht 426 Meter in die Höhe bewegen). Diese beiden Überlegungen verband Rudolf Clausius und folgerte, dass bei Dampfmaschinen offenbar nicht die gesamte Wärmeenergie in Bewegung umgesetzt wird; wäre dies der Fall, dann würde die dem System zugeführte Wärmeenergie mit der Umwandlung in Bewegung aus dem System verschwinden und nicht den Kondensator erhitzen. Da sich dieser jedoch erhitzt, bleibt ein Teil der Wärmeenergie offenbar ungenutzt und muss abgeführt werden. Diesen ungenutzten Anteil nannte er „Entropie“ und fasste seine diesbezüglichen Überlegungen 1850 im zweiten Hauptsatz der Thermodynamik zusammen.

Für den vorliegenden Zusammenhang ist von Bedeutung, dass die Entropie in einem abgeschlossenen System – also ohne Austausch von Energie oder Materie mit seiner Umgebung – gleich bleibt oder zunimmt, jedoch niemals geringer wird. Erhitzt man beispielsweise einen Eisenstab an einem Ende, so kühlt der erhitzte Teil mit der Zeit ab, während sich der nicht erhitzte erwärmt. Nach einiger Zeit wird der Stab gleichmäßig warm sein (da er auch an seine Umwelt  Wärme abgibt, wird er sich seinerseits an die Umgebungstemperatur anpassen – ein Prozess, der hier allerdings vernachlässigbar ist). Der Prozess verläuft immer von ungleichmäßig zu gleichmäßig und ist nicht umkehrbar. Im Gegensatz zu Bewegungen, die in der klassischen Mechanik beschrieben werden, ist die thermodynamische Entropieproduktion also irreversibel und besitzt eine eindeutige zeitliche Richtung.

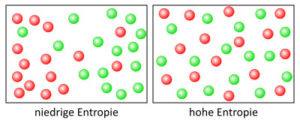Allerdings ist die zeitliche Richtung eine makroskopische Eigenschaft, die sich – wie Ludwig Boltzmann 1872 zeigte – auf mikroskopischer Ebene durchaus mechanistisch bzw. deterministisch beschreiben lässt. Er betrachtete Materie aus dem Blickwinkel der statistischen Mechanik als Ensemble sehr vieler einzelner Elemente (bzw. Atome) und beschrieb deren makroskopisches Verhalten mit Hilfe statistischer Methoden. So zeigte er, dass makroskopische Ordnung – z.B. ein Ende des Stabs kalt, ein Ende warm – mikroskopisch gesehen lediglich ein statistisch extrem unwahrscheinlicher Zustand ist. Stellt man sich also eine Menge „heißer“ und „kalter“ Atome an den unterschiedlichen Enden des Stabs vor (niedrige Entropie), die sich zufällig bewegen, so werden diese aus rein statistischen Gründen mit der Zeit gleichmäßig im Stab verteilt sein (hohe Entropie). Aus makroskopischer, phänomenaler Perspektive sind thermodynamische Prozesse also – wie ein „Zeitpfeil“ – zeitlich gerichtet bzw. asymmetrisch, in mikroskopischer Betrachtung sind sie symmetrisch und mit Methoden der klassischen Mechanik beschreibbar.

Spontane Strukturbildung im thermodynamischen Ungleichgewicht

Wenn also die Entropie eines Systems nur gleichbleiben oder zunehmen kann, dann müsste dieses irgendwann einen Endpunkt mit maximaler Entropie – sein thermodynamisches Gleichgewicht – erreichen. Nun ist die Erde allerdings alles andere als in einem thermodynamischen Gleichgewicht. Ganz im Gegenteil ist sie übersät mit Systemen, in denen hoch dynamische Prozesse ablaufen und die selbst sehr aktiv agieren und interagieren: lebende Zellen und Organismen.

Der Physiker Erwin Schrödinger wagte sich 1944 in den Bereich der Biologie vor und stellte  in einer populären und recht einflussreichen Publikation die Frage „Was ist Leben? – Die lebende Zelle mit den Augen des Physikers betrachtet“. Unter Bezug auf Boltzmanns thermodynamische Interpretation von Entropie stellt er fest, dass lebende Organismen ganz wesentlich dadurch gekennzeichnet sind, dass sie ständig mit ihrer Umwelt Stoffe austauschen und dadurch die laufend in ihrem Inneren produzierte Entropie an ihre Umwelt abgeben:

„Ein Organismus erscheint deswegen so rätselhaft, weil er sich dem raschen Verfall in einen unbewegten »Gleichgewichtszustand« entzieht, und dieses Rätsel hat der Menschheit so viel zu schaffen gemacht, daß sie seit den frühesten Zeiten des philosophischen Denkens und teilweise auch heute noch behauptet, im Organismus sei eine unkörperliche, übernatürliche Kraft wirksam (vis viva, Entelechie). Wie entzieht sich der lebende Organismus dem Zerfall? Die Antwort lautet offenbar: Durch Essen, Trinken, Atmen und (im Falle der Pflanzen) durch Assimilation. … Jeder Vorgang, jedes Ereignis, jedes Geschehen … bedeutet eine Vergrößerung der Entropie jenes Teiles der Welt, in welchem es vor sich geht. Damit erhöht ein lebender Organismus ununterbrochen seine Entropie – oder, wie man auch sagen könnte, er produziert eine positive Entropie – und strebt damit auf den gefährlichen Zustand maximaler Entropie zu, der den Tod bedeutet. Er kann sich ihm nur fernhalten, d. h. leben, indem er seiner Umwelt fortwährend negative Entropie entzieht. … Das, wovon ein Organismus sich ernährt, ist negative Entropie. Oder, um es etwas weniger paradox auszudrücken, das Wesentliche am Stoffwechsel ist, daß es dem Organismus gelingt, sich von der Entropie zu befreien, die er, solange er lebt, erzeugen muß.“ (Schrödinger, 1987. S. 102 f)

Einen ersten Schritt hin zum Verständnis solcher Ordnungsprozesse unternahm Alan Turing 1952 in seiner Arbeit „The Chemical Basis of Morphogenesis„, indem er ein mathematisch formuliertes Modell (Turing-Mechanismus) zur spontanen Entstehung von Strukturen in sogenannten „Reaktions-Diffusions-Systemen“ entwarf. Damit wollte er zeigen, wie sich unterschiedliche Musterungen im Fell von Tieren (z.B. Zebra oder Tiger) durch relativ einfache chemische Reaktionsprozesse spontan entstehen können.

„Diffusion“ meint zunächst einmal nur „Durchmischung“ und lässt sich auch auf entropiebildende Prozesse im Boltzmann’schen Sinn anwenden. Beispielsweise könnte man sich einen durch eine Scheibe getrennten Behälter vorstellen, in dem sich unterschiedlich gefärbtes Wasser befindet. Aufgrund ihrer thermischen Energie bewegen sich die Moleküle des Wassers in beliebige Richtungen, stoßen aneinander an und beeinflussen ihre Bewegungen gegenseitig nach den Grundgesetzen der klassischen Mechanik (Brownsche Bewegung). Entfernt man nun die Trennscheibe, so wird man mit der Zeit eine zunehmende Durchmischung des Wassers beobachten, bis sich schließlich eine homogene Flüssigkeit gebildet hat, die sich nicht mehr weiter verändert. Diese Durchmischung lässt sich mit Diffusionsgleichungen (mathematisch analog zu thermodynamischen Wärmeleitungsgleichungen) beschreiben.

Turing analysierte nun Moleküle, die mit unterschiedlichen Geschwindigkeiten diffundierten und die dabei chemisch miteinander reagierten. Um die Musterbildung auf Tierfellen mathematisch beschreiben zu können, nahm er zunächst an, dass zwei „Morphogene“ – ein Aktivator und ein Inhibitor – in Zellen die Produktion des Farbstoffs Melatonin anregen. Der Aktivator ist autokatalytisch (regt in der Zelle also auch die Produktion von zusätzlichen Aktivatoren an) und verbreitet sich langsam, der Inhibitor unterdrückt die Produktion von Aktivatormolekülen und verbreitet sich schnell.

Auch hier sollte man erwarten, dass sich irgendwann ein stabiler Gleichgewichtszustand mit einer gleichbleibenden Konzentration von Aktivator-und Inhibitormolekülen einstellt. Allerdings ist dies nicht unbedingt der Fall. Der für beide Morphogene unterschiedlich schnell verlaufende Diffusionsprozess kann vielmehr zu sogenannten „Turing-Instabilitäten“ führen und ist damit die Voraussetzung für die eine spontane Musterbildung. Je nach Parameter können diese Muster unterschiedliche Formen annehmen und sich unterschiedlich schnell verändern oder pulsieren. Im Gegensatz zum thermodynamischen Modell (s.o.) ist Diffusion hier also keine zufällig wirkende, ordnungszersetzende Kraft, sondern vielmehr eine zentrale Voraussetzung für die makroskopische Selbststrukturierung der Materie.

Um 1950, also etwa zur selben Zeit als sich der Mathematiker Turing mit der prinzipiellen Möglichkeit spontaner Strukturbildung beschäftigte, beobachtete der Chemiker Boris Belousov in einer Lösung mit mehreren chemisch reagierenden Substanzen spontan entstehende, oszillierende Strukturen. Da diese Strukturbildung dem zweiten Hauptsatz der Thermodynamik (s.o.) widersprach, wurde sie zunächst für einen Messfehler oder eine Verunreinigung gehalten und gelangte erst 1959 zur Veröffentlichung. Der Physiker Anatoli Zhabotinsky beschrieb dieses nun „Belousov-Zhabotinsky-Reaktion“ genannte Phänomen als Resultat chemischer Kreisprozesse, in dessen Verlauf einzelne Reaktionsbestandteile (Kaliumbromat, Malonsäure u.a.; eine genauere Beschreibung z.B. hier) chemisch immer wieder modifiziert werden und dabei ihr Farbe ändern. Anhand einer kleinen Simulation kann man selbst explorieren, wie sehr die Musterbildung von verwendeten Parametern abhängig ist.

Ab den 1940er Jahren beschäftigte sich auch Ilya Prigogine mit selbstorganisierenden Prozessen fern des thermodynamischen Gleichgewichts, z.B. dem relativ alltäglichen Phänomen der „Bénard-Zellen„: Erwärmt man eine Flüssigkeit in einem Topf von unten, so wird die zugeführte Wärme vom Boden zur Oberfläche geleitet und dort an die Umgebung abgegeben. Erhöht man nun die Wärmezufuhr – entfernte man das System also ein Stück weiter weiter vom thermodynamischen Gleichgewicht – , so ändert sich ab einem bestimmten Punkt plötzlich das Aussehen der Flüssigkeit und es bilden sich sichtbare Strukturen aus. Die Teilchen überwinden ihre innere Reibungskraft und formieren sich zu Konvektionsströmen, die die von unten zugeführte Wärme wesentlich schneller durch das System leiten und an der Oberfläche wieder abgeben können. An dieser Stelle wichtig: Auch wenn die obige Beschreibung eine Art Zweckmäßigkeiten nahelegt (besseren Wärmedurchleitung durch Konvektion), der Prozess entsteht spontan und ohne einen Dirigenten, der eine solche Zweckmäßigkeit hätte überwachen und anordnen können.

 

Prigogine (Nobelpreis 1977) bezeichnete solche Prozesse in (materiell bzw. energetisch) offenen Systemen fern des thermodynamischen Gleichgewichts als „dissipative Strukturen„.

Die Entropieänderung  dS eines offenen Systems setzt sich aus der inneren Entropieänderung dS_i (durch Austauschprozesse innerhalb des Systems) und der äußeren Entropieänderung dS_e (durch Austauschprozesse zwischen System und Umwelt) zusammen (dS = dS_i + dS_e; wogegen in einem geschlossenen System: dS = dS_i).

Inder Nähe des thermodynamischen Gleichgewichts – also bei geringen Temperaturunterschieden zwischen innen und außen – wird die zugeführte Wärme durch Diffusion oder ungeordnete Strömungsprozesse durch das System geleitet und an die Umgebung abgegeben.

Sobald eine kritische Temperatur überschritten wird, bricht die hohe strukturelle Symmetrie des Systems (gleichförmige Verteilung aller Teilchen) und es entsteht ein System geringerer Symmetrie mit typischen Strukturen. Dabei stellt sich ein relativ stabiles Fließgleichgewicht ein, in dem sich der Zu- und Abfluss von Materie bzw. Energie die Waage halten. Die in ihnen produzierte Entropie (s.o. zweiter Hauptsatz) wird dabei laufend an die Umwelt abgegeben.

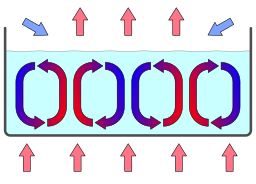
Die relative Stabilität erhält die Struktur durch den sich gegenseitig beeinflussenden Charakter zweier nichtlinearer Prozesse: Die dem System zugeführte Wärmeenergie bewirkt, dass die Flüssigkeitsmoleküle aufsteigen und die Wärmeenergie nach oben transportieren. Mit steigender Wärmezufuhr verstärkt sich diese Aufstiegstendenz bis es irgendwann durch geringfügige zufällige Schwankungen zum Symmetriebruch kommt. An irgendeiner Stelle steigen einige Moleküle gleichzeitig auf und jedes vorangegangene Molekül bahnt den Weg für nachfolgende Moleküle bis eine aufsteigende Strömung entsteht. Mehrere, nebeneinander angeordnete Konvektionsströme bilden makroskopisch stabile und mikroskopisch in ständigem Fluss befindliche Konvektionszellen. Diese Struktur wird durch die laufend zugeführte Wärmeenergie erhalten.

 

 

Literatur:

• Bischof, N. (1981). Aristoteles, Galilei, Kurt Lewin – und die Folgen. In: Michaelis, W. (Hrsg.): Bericht über den 32. Kongreß der Deutschen Gesellschaft für Psychologie in Zürich 1980. Bd. 1. Göttingen: Verlag für Psychologie. S. 17-39. Online-Link
• Bischof, N. (1990): Ordnung und Organisation als heuristische Prinzipien des reduktiven Denkens. In: Nova acta Leopoldina. NF 63, Nr. 272: S. 285-312. Online-Link
• Bischof, N. (2014). Psychologie – Ein Grundkurs für Anspruchsvolle. Stuttgart: Kohlhammer.
• Bischof, N. (2016). Struktur und Bedeutung – Einführung in die Systemtheorie. Bern: Hogrefe.
• Penzlin, H. (2012). Was heißt “lebendig”? Der Selbst-Organisation auf der Spur. Biologie Unserer Zeit, 1/2012 (42). Online-Link
• Schrödinger, E. (1989). Was ist Leben? Die lebende Zelle mit den Augen des Physikers betrachtet. München: Piper.

Interessantes:

• Brockmann, D. & Maier, B.F. (2018). „Hopfed Turingles“ – Pattern Formation in an Simple Reaction-Diffusion System. Complexity Explorables vom 30.12.2018. Online-Link
• Ewert, T. Die Welt der Strukturwissenschaften. Online-Link
• Hufsky, F. (2019). Turing-Mechanismen – Wie das Zebra zu seinen Streifen kommt. Bioinfowelten der Universität Jena vom 16.09.2019. Online-Link
• Hock, B. & Bolze, A. (1983). Die Zhabotinsky-Reaktion als Modell einer Musterbildung. Göttingen: IWF. Online Link
• Meinhardt, H. & Gierer, A. (1985). Aktivator-Inhibitor – Ein Modell zur biologischen Musterbildung. Göttingen: IWF. Online-Link
• Paeger, J. Was ist Entropie und wie steht diese im Zusammenhang mit Energie? Blog der Vorest AG. Online-Link
• Schuster, P. (2019). Von Erwin Schrödingers „Was ist Leben“ zu „Alles Leben ist Chemie“. Science Blog vom 21.11.2019. Online-Link
• Seara, D. (2018). How the Leopard got its Spots. Online-Link
• Schlichting, H. J. (2000). Von der Dissipation zur Dissipativen Struktur. Praxis der Naturwissenschaften – Physik 49/2, 12-16. Online-Link
• Sigmund, K. (2019). Als ein Physiker Ordnung ins Leben brachte – Erwin Schrödinger. Neue Zürcher Zeitung vom 01.11.2019. Online-Link
• Sims, Karl. Reaction-Diffusion Tutorial. Online-Link

AK 15.12.2022